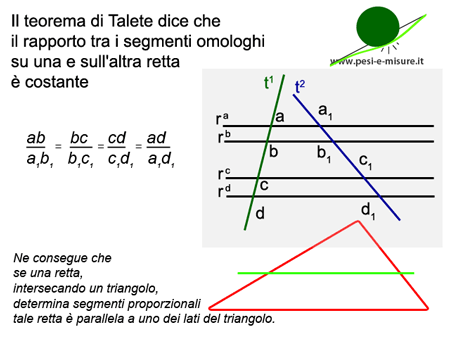
Enunciato del teorema di Talete: un fascio di rette parellele tagliate due rette trasversali intersecanti con esse determina due classi di segmenti proporzionali.
Su un piano poniamo un fascio di rette, nel nostro caso 4 rette che chiamiamo ra, rb, rc e rd
e le facciamo intersecare da due rette che chiamiamo t1 e t2
si formeranno i punti di intersezione a, a1, b, b1, c, c1, d, d1.
Questi punti sono delimitatori dei segmenti ab, bc, cd, a1b1, b1c1, c1d1.
Il teorema di Talete dice che il rapporto tra i segmenti omologhi su una e sull’altra retta è costante.
ab:a1b1 = bc:b1bc1
bc:b1bc1 = cd:c1d1
ab:a1b1 = cd:c1d1
vale anche per
ad:a1d1=ab:a1b1
Quindi ab/a1b1 = bc/b1c1 = cd/c1d1 = ad/a1d1
Ne consegue che se una retta, intersecando un triangolo, determina segmenti proporzionali, tale retta è parallela a uno dei lati del triangolo.