Il massimo comune pisore (M.C.D) tra due o più numeri è il più grande tra i pisori comuni a tali numeri, ovvero prendendo due numeri “m” e “n” è il numero più grande che pide sia m che n.
Il masssimo comune pisore si ottiene scomponendo i numeri in fattori primi e prendendo il prodotto dei soli fattori comuni presi una sola volta con l’esponente più basso.
MCD(m,n) si ottiene scomponendo m e n in fattori primi, prendendo il prodotto dei fattori primi comuni presi una sola volta con l’esponente più basso
Esempio:
m = 180 n = 270
Scomposizione in fattori primi:
180 | 2 270 | 2
90 | 2 135 | 3
45 | 3 45 | 3
15 | 3 15 | 3
5 | 5 5 | 5
1 1
m = 180= 22x32x5
n = 270= 2 x 33x5
MCD(180,270) = 2 x 32x 5 = 90
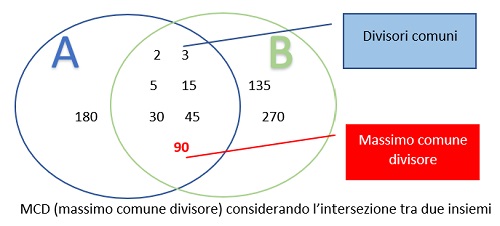
Rappresentazione del MCD (massimo comune pisore) considerando l’intersezione tra due insiemi:
A = {2, 3, 5, 15, 30, 45, 90, 180} (pisori del numero 180)
B = {2, 3, 5, 15, 30, 45, 90, 135, 270} (pisori del numero 270)
A Ո B = {2, 3, 5, 15, 30, 45, 90}