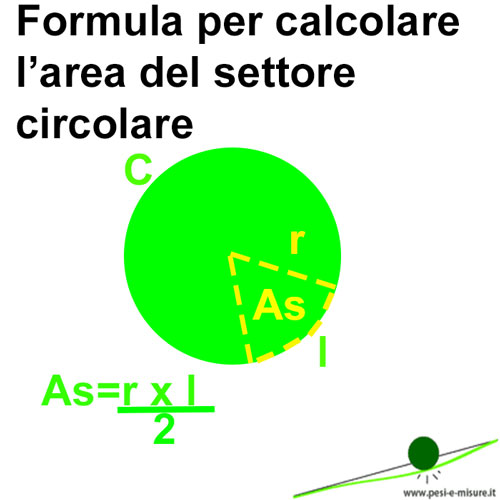
Formula per calcolare l’area del settore circolare
L’area del settore circolare (As) è un “pezzo” dell’area del cerchio delimitato da un arco (l) e da 2 raggi. Esso è appunto un pezzo dell’area del cerchio, cosi come l’arco è un pezzo della circonferenza.
Quindi per trovarlo si può utilizzare una proporzione: As ÷ A = l ÷ C
Altrimenti esiste una formula, derivante da questa proporzione: As= (A · l) ÷ C = (πr² ÷ l) ÷ 2rπ
Facendo pi greco diviso pi greco li si annula entrambi, così come facendo raggio alla seconda diviso raggio si fa scomparire l’esponente del dividendo e tutto il divisore.
Quindi diventa: As = (πr² · l) ÷ 2rπ= (r · l) ÷ 2
Di conseguenza esistono 2 modi per trovare l’area del settore circolare.
Per le formule inverse della proporzione basta utilizzare la proprietà delle proporzioni per trovare un’incognita ( un estremo o un medio).
Formula:
1) As ÷ A = l ÷ C
2) As = (r · l) ÷ 2
Formule inverse (solo seconda) :
l= (2 · A) ÷ r
r= (2 · A) ÷ l