Autore: antonio
-
Grammi, ettogrammi e chilogrammi. Tabella comparativa tra i pesi del sistema di pesatura metrico
Sistema di pesatura metrico mg milligrammi cg centigrammi dg decigrammi g grammi dag decagrammi hg ettogrammi kg chilogrammi Mg miriagrammi Q quintale T tonnellata mg cg dg g dag hg kg Mg q t 1 0,1 0,01 0,001 0,0001 0,00001 0,000001 0,0000001 0,00000001 0,000000001 10 1 0,1 0,01 0,001 0,0001 0,00001 0,000001 0,0000001 0,00000001 100…
-
Formula per calcolare la diagonale di un parallelepipedo
Formula per la diagonale di un parallelepipedo rettangolo Per calcolare la diagonale di un parallelepipedo rettangolo bisogna ricorrere ancora una volta al Teorema di Pitagora. Nel nostro caso il triangolo rettangolo preso in considerazione ha come cateti l’altezza del solido e la diagonale della base. Quindi per trovare l’ipotenusa di questo triangolo (ossia la diagonale…
-
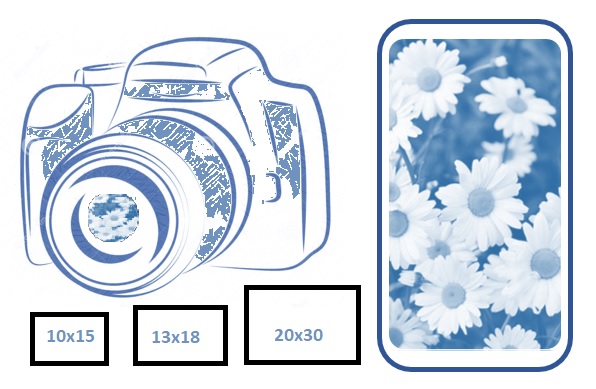
Formati stampe fotografiche standard in centimetri e in pixel
Da tempo ormai si fanno fotografie fatte digitalmente con vari dispositivi pronte da essere archiviate su memorie di vario genere, pc o cloud.Non dovendo più affidarci al rullino fotografico e potendole guardare, eliminare e scegliere quelle che più ci piacciono ne stampiamo a quantità. Ma è ancora bello avere una copia stampata in casa da…
-
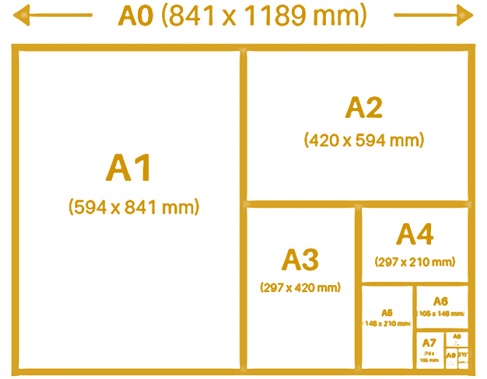
Dimensione e rapporto dei formati standard dei fogli di carta serie A
Non vi siete mai chiesti a che misure corrisponde la sigla scritta A4 posta sui pacchi di carta che si comprano per le fotocopiatrici o per le stampati collegate ai pc? Anzi, più che pacchi le confezioni fanno riferimento a risme di carta nel formato A4. Ma questo A4 in cm o in millimetri a…
-
mcm Minimo comune multiplo
Il minimo comune multiplo (m.c.m.) tra due o più numeri è il più piccolo tra i multipli comuni a tali numeri, ovvero prendendo due numeri “m” e “n” è il numero più piccolo multiplo sia di m che n. Il minimo comune multiplo si ottiene scomponendo i numeri in fattori primi e calcolando il prodotto…
-
Tavola pitagorica per imparare le tabelline
La TAVOLA PITAGORICA per imparare le tabelline ha accompagnato molti nelle prima fasi di apprendimento della matematica. La tavola è utilizzata come aiuto schematico per imparare a fare le moltiplicazioni. Inoltre con essa si comprende che moltiplicando 3×5 o moltiplicando 5×3 si ottiene sempre lo stesso risultato. Chi ha qualche hanno si ricorderà delle pertenti…
-
Relazione tra volume e capacità
La relazione tra volume e capacità chiarisce quando si dovrebbe utilizzare mc (metri cubo) e quando utilizzare l (litro) per definirne la misura di un corpo. Volume e capacità sono due metodi utilizzati spesso per misurare la stessa grandezza. La differenza tra i due possiamo definirla come segue:
-
Formula per calcolare la velocità, lo spazio ed il tempo
La velocità non è altro che il rapporto tra lo spazio percorso e il tempo necessario per percorrere tale spazio. La formula per ottenere la velocità è: V = S / T (spazio diviso tempo) Conoscendo la velocità ed il tempo utilizzato per percorrere un ipotetico spazio, si può ottenere lo spazio: S = T…
-
Misure dirette e indirette
La misurazione di un determinato misurando può essere fatta con metodo diretto o metodo indiretto. Misurare con metodo diretto Misurare una grandezza con metodo diretto significa ottenere il valore del misurando confrontadolo direttamente con l’unità di misura (campione) o suoi multipli o sottomultipli. I valori ottenuto con le misurazioni che si fanno quotidianamente con righelli…
-
Misurare e misurazione – significato
Misurare e misurazione – significato Con la misurazione andiamo ad attribuire un intervallo di valori ad una grandezza fisica detta misura. Misurare una grandezza significa trovare il rapporto tra essa ed una grandezza dello stesso tipo, assunta come unità di misura, per stabilire quante volte quest’ultima è contenuta nella grandezza che vogliamo misurare. Per “grandezza…
-
MCD Massimo comune divisore
Il massimo comune pisore (M.C.D) tra due o più numeri è il più grande tra i pisori comuni a tali numeri, ovvero prendendo due numeri “m” e “n” è il numero più grande che pide sia m che n. Il masssimo comune pisore si ottiene scomponendo i numeri in fattori primi e prendendo il prodotto…
-
La geometria, gli enti fondamentali
La geometria, gli enti fondamentali Come si è detto nella definizione di Geometria, per studiare ed esaminare le proprietà degli oggetti è necessario conoscere gli enti fondamentali alla base della geometria definiti da Euclide: Essi sono: Il punto Il punto è il primo ed il più semplice degli enti geometrici fondamentali. Esso è privo di…
-
Cos’è la geometria
Cos’è la geometria. Prendere le misure di oggetti, calcolare la dimensione degli spazi che occupano, studiarne la forma, analizzare gli oggetti nel contesto in cui si trovano per valutarne la posizione e lo spostamento.Tutte valutazioni e operazioni che facciamo quando ci troviamo di fronte sia a grandi che piccoli progetti disegnando righe, fissando punti e…
-
Il Rapporto tra enti geometrici fondamentali
Il Rapporto tra enti geometrici fondamentali Esistono dei rappoti tra gli enti geometrici fondamentali Punto, Retta e piano. Per stabilire i rapporti occore ricordare che il Punto non ha dimensioni, la retta ha come dimensione solo la lunghezza mentre il piano ha per dimensioni lunghezza e larghezza. Retta e piano sono concepiti come di dimensioni…
-
La geometria – Gli Assiomi o postulati
La geometria – Gli Assiomi o postulati, verità lapalissiane della geometria. L’assioma, per definizione, è una verita evidente che non ha bisogno di essere dimostrata. E’ una verita che non ammette discussione. Gli assiomi, che si postula ammessi per veri, sono necessari per fondare le argomentazioni tematiche in questo caso geometriche. Sono alla base della…
-
Il secondo, unità di misura del tempo.
Il secondo, unità di misura del tempo. Il secondo, nel sistema internazione, è l’unità di misura utilizzata per definire la grandezza “tempo”. E’ definito come il tempo di 9 192 631 770 periodi della radiazione emessa, in certe condizioni ben definite dello stato dell’atomo di cesio-133 E’ un sistema di misura misto in quanto usa…
-
Il piano cartesiano
Il piano cartesiano, sistema di riferimento su due dimensioni Il sistema cartesiano permette di associare i punti di un piano con i numeri. E’ un sistema studiato dal matematico René Descartes. Il piano cartesiano è rappresentato da due rette perpendicolari dette “assi cartesiani”. Una orientata verso destra definita “asse delle ascisse” e indicata dal simbolo”x” …
-
Tabella dei pesi specifici
La tabella che segue elenca i pesi specifici di alcuni tra i materiali più comuni espressi in grammi per centimetri cubi. Note: I valori indicati possono essere considerati anche come chilogrammi per decimetri cubi in quanto dire che 1 cm3 di olio d’oliva pesa 0,916 g è lo stesso che dire che 1 dm3 della…
-
Il peso specifico
Il peso specifico di una sostanza (o di un corpo) corrisponde al suo peso espresso in kg per dm3. I pesi specifici di varie sostanze vengono calcolati sulla base di un volume uguale chiamato peso per unità di volume. Il cacolo del peso specifico si effettua rapportando il Peso (in kg) con il Volune(dm3): Ps…
-
Tabella di conversione e rapporto tra le lunghezze nel sistema di misura in metri
Tabella di conversione e rapporto tra le lunghezze nel sistema di misura in metri (multipli e sottomultipli del metro) mm -> millimetri cm -> centimetri dm -> decimetri m -> metri dam -> decametri hm -> ettometri km -> chilometri mm cm dm m dam hm km 1 0,1 0,01 0,001 0,0001 0,00001 0,000001 10…
-
Il metro, umità di misura delle lunghezze del sistema metrico decimale.
Il metro è l’unità di misura delle lunghezze del sistema metrico decimale. Era definito come la quarantamilionesima parte della lunghezza del meridiano terrestre passante per Parigi. Per poter stabilire e controllare con precisione la sua lunghezza si rese necessario creare un campione. Questo campione è tuttora conservato nell’Ufficio pesi e misure a Sèvres (Parigi). Il…
-
Rapporto tra il metro quadrato e i suoi multipli e sottomultipli
Rapporto tra il metro quadrato e i suoi multipli e sottomultipli. km² -> chilometri quadrati hm² -> ettometri quadrati dam² -> decametri quadrati m² -> metri quadrati dm² -> decimetri quadrati cm² -> centimetri quadrati mm² -> millimetri quadrati m² dm² cm² mm² 1 100 10.000 1.000.000 0,01 1 100 10.000 0,0001 0,01 1 100…
-
Il metro quadrato, unità di misura della superficie
Il metro quadrato, unità di misura della superficie. Il metro quadrato (m2) è l’unità di misura base per la superficie. Corrisponde alla superficie di un quadrato con il lato lungo un metro. Il metro quadrato si definisce una unità di misura derivata in quanto si ottiene dal metro. Le equivalenze con il metro quadrato procedono…
-
Rapporto volumetrico tra metri cubi e sottomultipli
Rapporto volumetrico tra metri cubi e sottomultipli mᶾ metri cubi dmᶾ decimetri cubi cmᶾ (cc) centimetri cubi mmᶾ millimetri cubi mᶾ dmᶾ cmᶾ (cc) mmᶾ 1 1.000 1.000.000 1.000.000.000 0,001 1 1.000 1.000.000 0,000001 0,001 1 1000 0,000000001 0,000001 0,001 1
-
Il metro cubo, unità di misura del volume
Il metro cubo, unità di misura del volume. Il metro cubo (m3) è l’unità di misura base per il volume. Corrisponde alla superficie di un cubo con lo spigolo lungo un metro. Il metro cubo si definisce una unità di misura derivata in quanto si ottiene dal metro. Le equivalenze con il metro cubo procedono…
-
Il grado unità di misura degli angoli
L’unità di misura degli angoli è il grado (°). UM Simbolo Grado ° Primo ‘ Secondo “ Il grado è definito come la “360ma parte di un angolo giro” e ne misura l’ampiezza. Il sistema per misurare l’ampiezza degli angoli è chiamato “sessagesimale“, sistema di numerazione in base 60 dove ogni unità corrisponde a 60…
-
Grandezze proporzionali
Grandezze proporzionali Nel nostro quotidiano si parla di grandezze costanti quando queste hanno un valore che non si altera nel tempo e di grandezze variabili quando queste cambiano valore in base alle situzioni in cui vengono definite. La capacità di una bottiglia, ad esempio, è una grandezza costante mentre la capacità di un palloncino, essendo…
-
Grandezze proporzionali – problema del tre semplice
Grandezze proporzionali – problema del tre semplice Il problema del tre semplice lo si ha quando si conoscono tre valori e si necessita di calcolare il vaolre del quarto. La risoluzione dei problemi del tre semplice è un’applicazione del concetto di grandezze direttamente proporzionali e grandezze inversamente proporzionali. Quando le due grandezze di riferimento…
-
Grandezze proporzionali – problema del tre composto
Il problema del tre composto è un argomento che fa parte dei calcoli proporzionali. Si presenta quando si è a conoscenza dei valori di tre grandezze. Per capire la modalità di calcolo ci baseremo sull’analisi seguente esempio: per raccogliere 100 kg di mele occorrono 10 persone per 2 ore. Quanti kg di mele possono raccogliere…
-
Grandezze inversamente proporzionali
Grandezze inversamente proporzionali Nelle grandezze inversamente proporzionali, se la prima aumenta, la seconda diminuisice. Oppure se la prima diminuisce la seconda aumenta. Ad esempio, prendendo in considerazione un automobile in movimento, l’auto può percorrere la stessa distanza in tempi persi a seconda della velocità. Per percorrere 20 km sono necessari 20 minuti a 60 km/h…