Autore: antonio
-
Formula per calcolare l’area della corona circolare
Formula per calcolare l’area della corona circolare L’area della corona circolare è la differenza tra l’area di 2 cerchi concentrici, cioè di stesso centro. Quindi si potrebbe scrivere : Acor = A1 – A2 Altrimenti si potrebbe ottenere un’altra formula derivante da questo ragionamento: A1 – A2 = πR2 – πr2 Utilizzando il raccoglimento a…
-
Formula per calcolare l’area del triangolo con la formula di Erone
Formula per calcolare l’area del triangolo con la formula di Erone Se sono note le misure dei tre lati e non si conosce l’altezza è possibile calcolare l’area del triangolo mediante la formula (indiretta) di Erone. Formula di Erone: L’area di un triangolo di cui sono note le misure dei lati è uguale alla radice…
-
Formula per calcolare l’area del triangolo
L’area del triangolo si ottiene moltiplicando la base per l’altezza e dividendo il prodotto per due. Formula: (b x a) / 2 Per il concetto di equivalenza tra le figure piane Il triangolo è equivalente alla metà di un parallelogrammo avente la stessa base e la stessa altezza.
-
Formula per calcolare l’area del trapezio
Formula per calcolare l’area del trapezio Il trapezio è un quadrilatero avente le 2 basi opposte parallele. L’area del trapezio si calcola dividendo per 2 il prodotto tra la somma delle basi e l’altezza. Formula: A=[(B+b) · h] ÷ 2 Formule inverse
-
Formula per calcolare l’area del settore circolare
Formula per calcolare l’area del settore circolare L’area del settore circolare (As) è un “pezzo” dell’area del cerchio delimitato da un arco (l) e da 2 raggi. Esso è appunto un pezzo dell’area del cerchio, cosi come l’arco è un pezzo della circonferenza. Quindi per trovarlo si può utilizzare una proporzione: As ÷ A =…
-
Formula per calcolare l’area del segmento circolare a una base a cui non appartiene il centro
Formula per calcolare l’area del segmento circolare a una base a cui non appartiene il centro. Un segmento circolare è una porzione di cerchio delimitata da una corda, che può contenere o no il centro. Per calcolarne l’area, quando il centro non è al suo interno, si deve sottrarre all’area del settore circolare, dove esso…
-
Formula per calcolare l’area del rombo
Uno dei metodi per calcolare l’area del rombo è quello di moltiplicare tra loro la lunghezza delle 2 diagonali e dividere il prodotto per 2. Formula: (d1 x d2)/2
-
Formula per calcolare l’area del rettangolo
IL rettangolo è una figura geometrica piana a 4 lati, uguali a 2 a 2. I lati uguali sono uno opposto all’altro. Per calcolare la dimensione dell’area del un rettangolo è necessario conoscere e moltiplicare tra loro la misura della lunghezza della base per la misura dell’altezza. La formula è: A = b x a
-
Formula per calcolare l’area del quadrato
L’area di un quadrato si calcola moltiplicando il lato corrispondente alla base moltiplicato al lato corrispondente all’altezza. Avendo i 4 lati di dimensione uguale, la formula per il calcolo dell’area diventa “lato per lato”, oppure “lato elevato al quadrato”. Le formule sono: A = lxl A = l² Al contrario, se si conosce l’area e…
-
Formula per calcolare l’area del parallelogrammo
Formula per calcolare l’area del parallelogrammo L’area del parallelogramma si calcola moltiplicando la misura della base per quella dell’altezza. Formula: A = b x a Formule inverse: b = A:h h = A:b Per il concetto di equivalenza tra le figure piane, il parallelogrammo è equivalente a un rettangolo avente la stessa base e la…
-
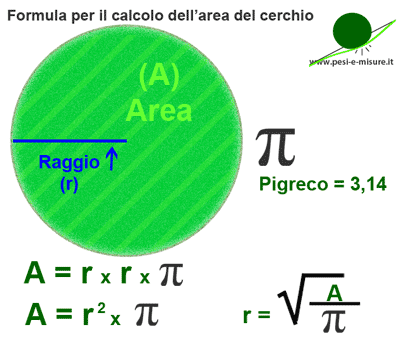
Formula per calcolare l’area del cerchio
Nella pagina dedicata alla formula per calcolare la circonferenza del cerchio si era definito come il cerchio prende la sua forma, la sua sagoma.Nella definizione si diceva che, dato un punto, il cerchio è una figura geometrica piana delimitata da un insieme di punti equidistanti dal punto dato detto centro. L’insieme di punti formano una…
-
Formula per calcolare il volume di un cono
Il cono è una forma geometrica solida ottenuta dalla rotazione di un triangolo sul suo cateto. Il volume di un cono corrisponde alla terza parte del volume di un cilindro e si calcola dividendo per tre il risultato della moltiplicazione di pigreco per raggio al quadrato, per altezza. Formula: pigreco x r² x altezza /…
-
Formula per calcolare il volume della sfera
Per calcolare il volume di una sfera occorre conoscere la dimensione del raggio. Elevare tale dimensione al cubo, moltiplicarla per pigreco e moltiplicare per il risultato di 4 diviso 3. V = 4/3 x pigreco x r³ Note: Il Pigreco corrisponde al rapporto tra Circonferenza e diametro (Pigreco = C/d = 3,14)
-
Formula per calcolare il volume della piramide
La piramide è un solido avente come base un poligono e tante facciate triangolari, che puntano allo stesso vertice, quanti sono i lati del poligono. A seconda che la base sia a forma di triangolo, quadrilatero o pentagono, la piramide si definisce a base triangolare, quadrangolare, pentagonale, ecc. Il volume della piramide, qualsiasi sia la…
-
Formula per calcolare il volume del parallelepipedo rettangolo
Il volume del parallelepipedo rettangolo si calcola moltiplicando l’area della base per l’altezza. Formula: lunghezza x larghezza x altezza
-
Formula per calcolare il volume del cubo
Il cubo è una figura a tre dimensioni con 6 facciate, di forma quadrata, di uguale superficie. Il volume del cubo si calcola elevando al “cubo” (alla terza) la lunghezza del lato di uno qualsiasi dei quadrati che formano le facciate. In pratica “lato x lato x lato” La formula: V = l³ Dal volume…
-
Formula per calcolare il volume del cilindro
Il cilindro è un solido generato dalla rotazione completa di un rettangolo (figura piana) attorno ad uno dei suoi lati. Ruotando, sulla superficie piana su cui ruota, forma un cerchio il cui raggio è il lato della base del rettangolo. Il cerchio che si è formato è la base del cIlindro. Per calcolare il volume…
-
Formula per calcolare il peso di un foglio di carta
Quanto pesa un foglio di carta? Il peso teorico di un foglio di carta cambia a seconda della grammatura di cui è composto. Partendo dal presupposto che la grammatura carta, per convenzione, si riferisce al peso espresso in grammi di un foglio la cui superficie è pari ad un metro quadrato, ne deriva che per…
-
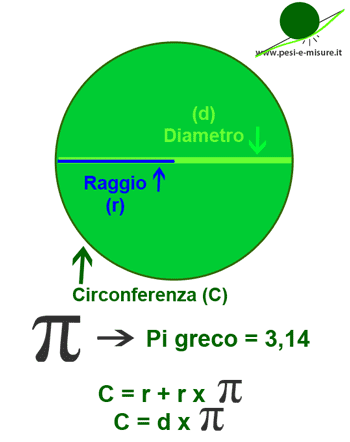
Formula per calcolare il perimetro, o circonferenza, del cerchio
Cos’è un cerchio? Dato un punto, il cerchio è una figura geometrica piana delimitata da un insieme di punti equidistanti dal punto dato detto centro. L’insieme di punti formano una linea curva chiusa chiamata circonferenza. Ma come si calcola la circonferenza, la lunghezza della linea chiusa ovvero il perimetro della figura geometrica? Per calcolare la…
-
Formula per calcolare l’area dell’ellisse
A = a x b x pigreco (3,14) Breve introduzione su cos’è un’ellisse L’ellisse è una curva dall’aspetto ovale che prende una precisa forma e dimensione in base a riferimenti dati. Per capire come si disegna un ellisse prendiamo come esempio la “costruzione del giardiniere”, la tecnica che si usa per costruire le aiuole. Definiamo…
-
Formula per calcolare il perimetro dell’ellisse
Formule per il calcolo del perimetro dell’ellisse:P = Pigreco x radicequadrata di 2 x a2 x b2 (pigreco per radice quadrata di semiassemaggiore al quadrato per semiasseminore al quadrato)P = 2 x Pigreco x radicequadrata di (a2 x b2 /2) (2 per pigreco per radice quadrata di semiassemaggiore al quadrato per semiasseminore al quadrato diviso…
-
Formula per calcolare il numero di accoppiamenti possibili da x argomenti
Formula per calcolare il numero di accoppiamenti possibili da x argomenti. La formula per calcolare il numero massimo di accoppiamenti possibili tra “x” argomenti è la seguente:X(X-1)/2 = Y (“x” moltiplicato per “x”-1, dividendo il risultato per 2) Esempi: Date due lettere A e B, quanti accoppiamenti si possono fare tra loro?Applicando la formula: 2(2-1)/2…
-
Formula per calcolare il lato del trapezio isoscele col Teorema di Pitagora
Formula per calcolare il lato del trapezio isoscele col Teorema di Pitagora Tracciando l’altezza di un trapezio isoscele si può creare un triangolo rettangolo avente per ipotenusa il lato del trapezio e per cateti l’altezza e la proiezione del lato sulla base maggiore. Per calcolare la misura del lato del trapezio isoscele basta utilizzare il…
-
Formula per Calcolare il peso specifico
Il peso specifico di un corpo, sia esso liquido o solido, differisce da una sostanza all’altra a secondo del rapporto esistente tra peso e volume dello stesso. Ne consegue che, conoscendo peso e volume di un materiale, il relativo peso specifico si ottiene pidendo il peso per il relativo volume. Per definizione il peso specifico di un…
-
Formula per calcolare la proporzione e il valore del termine incognito
Formula per calcolare la proporzione e il valore del termine incognito.. Vi ricordate la maestra a scuola? Se 2 galline fanno 4 uova, 3 galline quante uova fanno? Ci chiedeva, in modo semplice, di eseguire una proporzione per calcolare il termine incognito. In termini matematici, dove i numeri 2,4,3 sono i tre termini conosciuti della…
-
Teorema di Euclide – secondo
Secondo teorema di Euclide, primo e secondo enunciato. Primo Enunciato: in un triangolo rettangolo il quadrato costruito sull’altezza relativa all’ipotenusa è equivalente al retangolo che ha per lati le proiezioni dei cateti sull’ipotenusa. Secondo Enunciato: in un triangolo rettangolo l’altezza relativa all’ipotenusa è media proporzionale tra le proiezioni dei cateti. Dimostrazione: Partendo da un triangolo…
-
Primo teorema di Euclide
Enunciato: In un triangolo rettangolo, il quadrato costruito su un cateto è equivalente al rettangolo che ha per dimensioni l’ipotenusa e la proiezione del cateto sull’ipotenusa. Partendo da un triangolo “ABC” poggiato sull’ipotenusa “AC”, costruiamo sui cateti “AB” e “BC e sull’ipotenusa “AC” dei quadrati che hanno per lato i detti segmenti. Tracciamo dal vertice…
-
Teorema di Talete
Enunciato del teorema di Talete: un fascio di rette parellele tagliate due rette trasversali intersecanti con esse determina due classi di segmenti proporzionali. Su un piano poniamo un fascio di rette, nel nostro caso 4 rette che chiamiamo ra, rb, rc e rd e le facciamo intersecare da due rette che chiamiamo t1 e t2…
-
Teorema di pitagora
In un triangolo rettangolo, l’area del quadrato costruito sull’ipotenusa (c2) è uguale alla somma dell’area dei quadrati costruiti sui cateti (a2 + b2) Calcolo dell’area del quadrato costruito sull’ipotenusa (c2): c2 = a2 + b2 Calcolo della lunghezza dell’ipotenusa (c): c = √ a2 + b2 (La lunghezza dell’ipotenusa “c” corrisponde alla radice quadrata della somma delle aree dei quadrati costruiti…
-
Il nodo, unità di misura della velocità del vento e le sue corrispondenze in miglia marine, km e metri
Il nodo (kn) è l’unità di misura della velocità del vento utilizzata a livello internazionale. Corrisponde a 1,852 km/h, misura derivante dalla distanza in metri percorsi in 1 miglio marino/h a cui, a livello internazionale, vengono attribuiti 1.852 mt.. Ne consegue che: Nodi(kn) Miglia(nm) Km m m/s 1 1 1,852 1.852 0,5144